PROPIEDAD DE REFLEXIÓN DE LAS CURVAS CÓNICAS
(LA ELIPSE)
¿Quien dijo que la matemática es muy difícil de aplicar a la vida diaria? Pues para aquellos que creen que las matemáticas no tienen aplicaciones SUPER INTERESANTES Y CURIOSAS aquí les dedico una pequeñisima muestra del inconmensurable poderío que las matemáticas ejercen en el desarrollo tecnológico actual y futuro y el auxilio que presta a otras disciplinas científicas.
(Con éste articulo, el blog Ciencia de BarceDavid participa en la VI edición del carnaval de matemáticas cuyo anfitrión sera el blog Sangakoo)
Cualquier estudiante de bachillerato (o preparatoria como se le conoce en otros países) ha estudiado alguna vez en su vida académica las comúnmente conocidas como secciones cónicas o simplemente "las cónicas" y dentro de éstas la que nos interesa ahora... LA ELIPSE.
Conviene que recordemos pues algunas de sus definiciones para nuestros propósitos.
Definición: La elipse es un lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una contante positiva. Una elipse es la curva cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado. (fuente: wikipedia)

El cociente c/a recibe el nombre de excentricidad (donde a es la mitad de la suma (o la semisuma) de las distancias de los focos F1 y F2 al punto P, y c es el centro de la la elipse)- El punto (h , k) situado a la mitad del camino entre los focos se llama centro
- Los puntos de intersección de una elipse y la recta que pasa por los focos se llaman vértices
- El segmento de recta que une los vértices es el eje mayor
- La parte de la recta que pasa por el centro perpendicularmente al eje mayor e intersecada por la elipse es el eje menor

Con esta sencilla, pero necesaria introducción ya estamos listos para saber como una cónica puede ser capaz de disolver cálculos renales.
Toda elipse tiene una notable propiedad de reflexión. Supóngase por ejemplo que un rayo de luz parte de uno de los focos y se dirige en línea recta hacia cualquier punto de la elipse, este rayo se reflejara en la elipse como si se estuviese reflejando en la recta tangente a la elipse en ese punto, después de reflejarse viajará en otra línea recta, y lo hará de tal modo que pasará por el otro foco.
En otras palabras, los rayos provenientes de uno de los focos de una elipse se reflejan en dirección al otro foco. Sean F y G los focos de una elipse. El siguiente gráfico muestra un punto P sobre la elipse y la recta tangente a la elipse en P. El ángulo que forma el "rayo incidente" FP con la recta tangente es igual al que forma el "rayo reflejado" GP del otro lado.
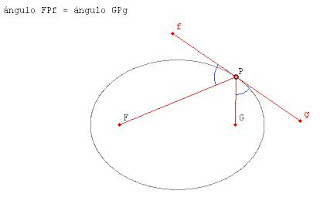
Esta propiedad de reflexión es la base del novísimo método de ultrasonido para disolver cálculos renales.
Se hace una tina rotando una elipse alrededor de su eje mayor. En esa tina, el paciente se coloca de manera que el cálculo quede situado exactamente en uno de los focos de la elipse, mientras que en el otro foco se coloca una fuente de vibraciones sónicas. Cuando esta fuente se enciende, todas las vibraciones se reflejan en las paredes de la tina y se concentran en el cálculo que afecta al paciente deshaciéndolo o triturándolo.
Falta por saber que opinaría algún profesional de la medicina luego de leer este brevisimo tratado sobre secciones cónicas y sus poderosos recursos para disolver cálculos renales... y algún paciente que se decida a probar esta tecnología.
¿alguien se anima?
saludos cordiales
B. David
FUENTES:
- Algebra de Rees - Sparks - Rees (10ma edición)
- http://centros.edu.xunta.es/



tengo que hacer una cuento animado secciones conicas
ResponderEliminarTe deseo exito en tu cuento animado de secciones conicas, perdon por responder tarde. Saludos cordiales.
Eliminar