MATEMATICAS APLICADAS A LA VIDA REAL

MUY INTERESANTE

Este video nos muestra una pequeña aplicación de probabilidades al momento de seleccionar un premio de entre tres lugares en los que podria estar, ¿como acertar (o tener mayores posiblidades de hacerlo) en un concurso en donde debes seleccionar donde esta el premio mayor?

Aqui la respuesta.

FELIZ NAVIDAD 2010

y saludos cordiales a todos.

Matemáticas aplicadas a la vida real - Muy interesante
Miguel Ángel Sabadell nos trae en esta nueva píldora de MuyTV como aplicar las matemáticas al día a día. ¿Dónde deberías invertir? ¿Qué caja tienes más posibilidades de tener premio en un juego de trileros? Descúbrelo en MuyTV

Palabras clave:vídeos experimentos muytv matemáticas

Vídeo de pildorasmuy

GEOMETRÍA EUCLIDIANA PARA DAR CON EL TESORO PERDIDO DE ATAHUALPA; EL ÚLTIMO DE LOS EMPERADORES INCAS.

(Esta entrada participa en la IX edición del carnaval de matemáticas cuyo anfitrión es sentado en la trebede)

TESOROS.... ¿a quien no le gustaría hallar uno? hay quienes prefieren encontrar tesoros usando viejos mapas, como en el libro de Julio Verne "Viaje al centro de la tierra" en donde vimos que el profesor Otto Lidenbrok al hallar una extraña criptografía en las hojas de un antiguo manuscrito, decide emprender viaje hacia el centro de la tierra a través del cráter del extinto volcán Snefls en Islandia... en busca del gran tesoro.

Mucho habrá que decir acerca de tesoros escondidos y recuperados y la importancia histórica y cultural que éstos representan para quienes los hallan y para el lugar a donde pertenecen, así por ejemplo las pirámides egipcias, los grandes buques llenos de oro hundidos en los mares atlánticos, los volcanes y llanos en la cordillera de los Andes o las dunas desérticas en Arabia contienen aún mucha información, tesoros  y escondites esperando aún ser descubiertos, pues bien, sudamerica y más en concreto Ecuador mi país posee quizá miles de sitios donde se dice existen grandes tesoros aun no descubiertos, ésta es la pequeña historia acerca del mayor de los tesoros aun no descubierto... EL GRAN TESORO PERDIDO DEL ÚLTIMO DE LOS EMPERADORES INCAS.

Podría escribir artículos enteros a explicar toda la historia en detalle, pero ese no es mi objetivo (a parte que no me simpatiza mucho la idea de los historiadores que escriben, escriben, y uno nunca sabe si sera o no absolutamente cierto lo que afirman...)  pero si haré una breve introducción acerca del mismo para luego pasar a presentar el problema que es la parte mas preciosa de este artículo, motivo de ésta IX edición del carnaval de matemáticas;  el mismo que nos dirá como hallar dicho tesoro.

UN POCO DE HISTORIA PARA COMENZAR CON EL RELATO....

Cuentan los libros de historia y las montañas sagradas de la cordillera de los Andes cuyas nieves perpetuas (ahora amenazadas por el calentamiento global) presenciaron dichos episodios que cuando estas tierras sudamericanas estaban siendo descubiertas y conquistadas por la Corona Española (en el caso de sudamerica y centroamerica) llegó el momento en que los conquistadores españoles se vieron obligados a enfrentar a peligrosas y temibles tribus indígenas e incáicas que dominaban estos territorios, así pues dadas las circunstancias y como en la mejor partida de ajedréz, los valientes conquistadores europeos capturaron al gran soberano y rey del territorio Inca, el poderoso ATAHUALPA, para cuyo rescate se pidió un cuarto lleno de oro y otro lleno de plata.

Cientos de nativos y esclavos empezaron a reunir en todo el territorio del Tahuantinsuyo tan preciados metales para rescate del desgraciado monarca Inca que cayó preso de los que el llamaba "hijos del sol" por su apariencia e instrumentos que usaban (armas de fuego), poco tiempo después sus captores se aburrieron y le dieron muerte al pobre monarca y al saberse de ésto, el poderoso y gran guerrero RUMIÑAHUI, nacido en estas tierras que ahora llamamos San Francisco de Quito (capital del Ecuador) decidió esconder todo el oro y plata reunidos para el rescate que jamas se concretó, pero lo hizo de tal forma que jamas nadie (se dice) podrá encontrarlo pues los conjuros con que fue guardado lo protejeran para siempre.

Para aquellos que les interese leer más acerca de la historia completa pueden dirigirse a esta página.

EL PROBLEMA DEL TESORO DE ATAHUALPA ESCONDIDO POR SU MEJOR GUERRERO.

¿como hallar dicho tesoro? he aquí la respuesta:

    

Se dice que Rumiñahui enterró el tesoro de Atahualpa en cierto lugar en el que existen una pirámide (P), un templo al sol (S) y una tumba (T) de tal modo que mirando desde la puerta del templo hacia afuera, la pirámide está a la izquierda y la tumba hacia la derecha. Para encontrar el tesoro hay que medir la distancia desde el templo hasta la tumba, luego girar en ángulo recto hacia la derecha, medir igual distancia y clavar una estaca (A). Luego medir la distancia y clavar otra estaca (B). El tesoro está enterrado precisamente en el centro de las dos estacas. Cierta persona tenía estos datos, mas cuando llegó al lugar no encontró ni rastro del templo al Sol y no pudo dar con el tesoro... sin embargo un estudiante de este libro bien pudo hallarlo. ¿como hacerlo?

Éste es un simpático ejercicio que está planteado en la sección POLIGONOS Y CUADRILATEROS en la GEOMETRIA PLANA Y DEL ESPACIO (de los autores: G. Calvache (mi maestro de geometría plana y esférica en el prepolitécnico de ingeniería) T. Rosero y M. Yacelga) profesores del área de ciencias básicas en la Escuela Politecnica Nacional del Ecuador.

En cierta ocación en uno de los deberes que me enviaron constaba este ejercicio... mas yo estudiante de aquel libro no pude dar con la solución correcta al problema, e incluso hay ocaciones en que se lo plantea en pruebas y examenes.

¿quien se anima a hallar teóricamente el gran TESORO DEL ULTIMO EMPERADOR INCA? yo lo intentare una ves mas

saludos cordiales

EL DESAFIO DEL ÚLTIMO TEOREMA DE FERMAT QUE NI EL DIABLO PUDO RESOLVER

(esta entrada participa en la IX edicion del carnaval de matemáticas que organiza en esta ocacion el blog sentado en la trebede)



Y aqui estamos nuevamente, el blog Ciencia de Barcedavid trae esta vez una curiosa historia relacionada con el último teorema de Fermat.... ese que ni el mismo Leonard Euler en su tiempo desordenando la casa de Fermat de arriba abajo pudo encontrar la "pequeña demostración para este problema de la cual Fermat decía que no cabía en el margen de su libro... realmente la hallo o no?

....En uno de los cuentos del libro Pactos con el Diablo de Arthur Poges, “El Diablo y Simón Flagg”, el diablo invita a Flagg a hacerle una pregunta difícil. Si el diablo la responde en 24 horas, el alma de Flagg será suya; si no, le regalará 100 mil dólares. La pregunta que Simón le hace es: “¿Es cierto el último teorema de Fermat?”. El diablo desaparece y al día siguiente reconoce su derrota: “Tú ganas, Simón —dijo casi en un susurro, mirándolo con un respeto absoluto—. Ni siquiera yo puedo aprender en tan poco tiempo las matemáticas requeridas para un problema tan difícil. Cuanto más indago sobre él, más difícil se torna”. Flagg sin duda fue astuto, veamos por qué.

Hace más de 300 años el genial matemático francés Pierre de Fermat, refiriéndose a un teorema que registró en su ejemplar de la Aritmética de Diofanto, escribió: “Poseo una demostración en verdad maravillosa para esta afirmación que no cabe en este estrecho margen”. Un teorema es una afirmación matemática que ha sido demostrada, fuera de toda duda, de modo que los matemáticos reconozcan la validez de la demostración (antes de que esto suceda, se trata sólo de una conjetura). La aseveración de Fermat sobre una atractiva afirmación matemática significó, por siglos, uno de los más grandes enigmas para los matemáticos. Tratando de “redescubrir” esa demostración del que ha sido conocido como el último teorema de Fermat, los matemáticos han recorrido muchos caminos, creando novedosas teorías, descubriendo nuevos teoremas, planteando interesantes conjeturas y, también, enfrentándose con grandes decepciones. Finalmente, en 1995, el enigma fue descifrado.

El matemático inglés Andrew Wiles, después de años de trabajo, logró encontrar una complicada, pero elegante demostración para este resultado. Por cierto, hoy en día nadie cree que Fermat haya tenido una demostración; por tanto, el último teorema de Fermat no lo fue sino hasta que Wiles lo demostró...

TEOREMA DE FERMAT:

Sea n > 3,  n elemento de los naturales; no existen números enteros distintos de cero X, Y, Z, tales que se cumpla la ecuación:

     n     n    n

X  + Y = Z

Demostración:
(este espacio es demasiado pequeño como para contener una demostracion de tan alto valor)

(fuente)

Propiedad Arquimediana de los Números Naturales

(esta entrada participa en la 7ma edición del carnaval de matemáticas cuyo anfitrión es el blog El Maquina de Turing)

Un teorema bastante "sencillo"

TEOREMA:

Sea "x" un número real positivo e "y" un número real cualquiera, entocnes existe un entero positivo "n" tal que nx>y

DEMOSTRACIÓN:

Puesto que el conjunto de los enteros positivos no es acotado superiormente, existe n elemento del conjunto de los enteros positivos tal que n > (y/x) de donde se sigue que nx >y ▄

La propiedad arquimediana de los números reales tiene la siguiente interpretación geométrica:

Si tenemos dos segementos de recta uno tan largo como queramos de longitud Z y el otro de lingitud tan corto como queramos de longitud X, tomando un número suficientemente el nuúero de veces el segmento pequeño, podemos cubrir el segmento grande asi:

________________________________________________
(segmento de longitu Z)


________
(segmento de longitu X)


Utilizando la propiedad arquimediana se puede demostrar con alguna dificultad y sin usar interpretaciones decimales que el conjunto de los números racionales es denso ( es decir que todos sus puntos son de acumulación) en el conjunto de los numeros reales, a partir de este último resultado se puede deducir también que el conjunto de los números irracionales también es denso en el conjunto de los reales. ▄

He escrito esta entrada especialmente para esta séptima edición del carnaval de matemáticas, disculpen ustedes amigos matemáticos la sencillez del mismo, hice lo mejor que pude en el corto tiempo que dispuse.

Saludos cordiales

EL COLMO DE UN OLVIDADIZO

JAMES JOSEPH SYLVESTER

En ocaciones, olvidamos cosas que usualmente son importantes para alguna de nuestras actividades diarias, éste fue el caso del matemático inglés James Joseph Sylvester que solia olvidar (tal era su grado de distracción) incluso algunos teoremas que debía volver a deducir frecuentemente para poder usarlos... sin embargo dentro de su campo fue uno de los mas grandes matemáticos ingleses del siglo XIX, éste es un breve ensayo de su interesante biografía.

Con esta entrada el blog Ciencia de BarceDavid participa en la VI edición del carnaval de matemáticas cuyo anfitrion es el blog Sangakoo)

Para el estudiante que tiene dificultad en recordar los teoremas podría consolarle el saber que almenos, uno de los mas grandes matemáticos tenia esas dificultades. El matemático inglés James Sylvester (1814 - 1897) que tanto se destacó en el siglo XIX tenía que deducir de nuevo y con mucha frecuencia los teoremas que había de utilizar, Una vez incluso objetó un teorema expuesto por un colega suyo insistiendo que nunca se había demostrado... resultó ser que él mismo había descubierto, demostrado y publicado en una revista.

Otro hecho que indica hasta donde llegaba su grado de distracción sucedió en una reunión pública cuando Sylvester que además tenía talento poético quizo recitarles un poema de 400 versos rimando todos con la palabra "Rosalind" Reunido ya con sus amigos para declamar el poema empezó explicando las notas aclaratorias, entusiasmándose tanto en sus pequeños detalles que no se dio cuenta del tiempo que transcurría ni del cansancio de sus oyentes. De pronto se dio cuenta que había hablado hora y media sin haber recitado ni una sola línea del poema.

Esto sucedió durante los años felices en que Sylvester vivió en la Universidad de Johns Hopkins. años atrás había rechazado bruscamente un profesorado en una universidad norteamericana debido a que el prefecto no había castigado a un estudiante en la forma en que Sylvester, un inglés pensaba era adecuado.

No obstante lo distraido que fue Sylvester, era un genio de la investigación matemática universitaria, fue una persona que en su época, trabajó para establecer los estudios y las investigaciones matemáticas para graduados de los Estados Unidos. Una de sus muchas contribuciones para el avance de las matemáticas fue la fundación de la revista norteamericana "American Journal of Mathematics"

UN POCO DE SU VIDA:

• Junto con Arturo Caley fundó la teoría de los invariantes algebraicos
• en 1838 Sylvester se hizo profesor de Filosofía Natural en la Universidad de Londres.
• en 1841 aceptó el profesorado de matemáticas en la Universidad de Virginia Charlottesville, fue relegado de sus funciones transcurridos tres meses de aquello; 4 años después viajo a Londres donde se inició como escribano para una compañía de seguros mientras solo retenía su interés en la matemática a través de la enseñanza.
• En 1846 se convierte en estudiante de derecho y jurisprudencia y más tarde trabajando como abogado Joseph empezó una sociedad amigable con Caley.
• Caley y Sylvester se conocieron en 1850 no como matemáticos sino como abogados, se hicieron muy amigos uno del otro, su relación tuvo influencia recíproca de la cual salió en favor de las matemáticas y en perjuicio de la jurisprudencia.
• Sylvester se conservó en la cátedra hasta el año 1870 en que fue jubilado por imperativo legal.
• Escribió un libro llamado "THE LAW OF VERSE" en 1870
• Joseph realizó una labor de divulgación matemática a través de la American Journal of Mathematics que fundó en 1875 provocando una verdadera revolución en la enseñanza de las matemáticas y cuando regreso en 1885 a Ingalterra com profesor de Oxford
• Pidió un puesto de trabajo en la escuela Militar de Woolwich el cual le fue negado lo que implico que siguiera trabajando en la compañía de seguros
• Permaneció unos años mas realizando una labor de burócrata, al haber una vacante en el Gresham Collage de Londres la solicitó pero se la negaron, en cambio fue solicitado por la Academia Woolwich para sustituir al candidato que lo habia derrotando antes.... porque éste acababa de morir.
  

B. David

FUENTES:

• GEOMETRÍA MODERNA (JURGENSEN - DONNELLY - DOLCIANI)

SECCIONES CÓNICAS QUE DISUELVEN... ¡¡¡CÁLCULOS RENALES!!!

PROPIEDAD DE REFLEXIÓN DE LAS CURVAS CÓNICAS

(LA ELIPSE)

¿Quien dijo que la matemática es muy difícil de aplicar a la vida diaria? Pues para aquellos que creen que las matemáticas no tienen aplicaciones SUPER INTERESANTES Y CURIOSAS aquí les dedico una pequeñisima muestra del inconmensurable poderío que las matemáticas ejercen en el desarrollo tecnológico actual y futuro y el auxilio que presta a otras disciplinas científicas.


(Con éste articulo, el blog Ciencia de BarceDavid participa en la VI edición del carnaval de matemáticas cuyo anfitrión sera el blog Sangakoo)

Cualquier estudiante de bachillerato (o preparatoria como se le conoce en otros países) ha estudiado alguna vez en su vida académica las comúnmente conocidas como secciones cónicas o simplemente "las cónicas" y dentro de éstas la que nos interesa ahora... LA ELIPSE.


Conviene que recordemos pues algunas de sus definiciones para nuestros propósitos.


Definición: La elipse es un lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una contante positiva. Una elipse es la curva cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado. (fuente: wikipedia)

• 
  El cociente c/a recibe el nombre de excentricidad (donde a es la mitad de la suma (o la semisuma) de las distancias de los focos F1 y F2 al punto P, y c es el centro de la la elipse)



• El punto (h , k) situado a la mitad del camino entre los focos se llama centro



• Los puntos de intersección de una elipse y la recta que pasa por los focos se llaman vértices



• El segmento de recta que une los vértices es el eje mayor



• La parte de la recta que pasa por el centro perpendicularmente al eje mayor e intersecada por la elipse es el eje menor

Con esta imagen animada, podemos observar la propiedad que caracteriza a una elipse, la suma de las distancias a dos puntos fijos llamados focos siempre es constante positiva.




Con esta sencilla, pero necesaria introducción ya estamos listos para saber como una cónica puede ser capaz de disolver cálculos renales.


Toda elipse tiene una notable propiedad de reflexión. Supóngase por ejemplo que un rayo de luz parte de uno de los focos y se dirige en línea recta hacia cualquier punto de la elipse, este rayo se reflejara en la elipse como si se estuviese reflejando en la recta tangente a la elipse en ese punto, después de reflejarse viajará en otra línea recta, y lo hará de tal modo que pasará por el otro foco.
En otras palabras, los rayos provenientes de uno de los focos de una elipse se reflejan en dirección al otro foco. Sean F y G los focos de una elipse. El siguiente gráfico muestra un punto P sobre la elipse y la recta tangente a la elipse en P. El ángulo que forma el "rayo incidente" FP con la recta tangente es igual al que forma el "rayo reflejado" GP del otro lado.





Esta propiedad de reflexión es la base del novísimo método de ultrasonido para disolver cálculos renales.
Se hace una tina rotando una elipse alrededor de su eje mayor. En esa tina, el paciente se coloca de manera que el cálculo quede situado exactamente en uno de los focos de la elipse, mientras que en el otro foco se coloca una fuente de vibraciones sónicas. Cuando esta fuente se enciende, todas las vibraciones se reflejan en las paredes de la tina y se concentran en el cálculo que afecta al paciente deshaciéndolo o triturándolo.

Falta por saber que opinaría algún profesional de la medicina luego de leer este brevisimo tratado sobre secciones cónicas y sus poderosos recursos para disolver cálculos renales... y algún paciente que se decida a probar esta tecnología.

¿alguien se anima?

saludos cordiales

B. David


FUENTES:

• Algebra de Rees - Sparks - Rees (10ma edición)
• http://centros.edu.xunta.es/

PROBLEMA DE SUCESIONES

Este ejercicio fue propuesto en el libro "MATEMÀTICAS, CURSO PREUNIVERSITARIO" cuyos autores son los matemáticos Sylvie Esquerré, Jorge Lara, Rolando Sáenz del Centro de Matemática de la Universidad Central del Ecuador.

Mucha dificultad, largas noches de cálculos, varios meses de fallido intento y mas de un dolor de cabeza me produjo este solo ejercicio que consta de 4 items, finalmente mi maestro el matemático Hernan Benalcazar que también pertenece al Centro de Matemática de la Universidad Central del Ecuador nos mostros que para dar soluciónes al mismo (lo resolvimos entre todos en un curso de análisis matemático I) se necesitan no menos de dos horas de tiempo... ¡ y a mi me lo pusieron para un examen final de matematicas basicas de una hora de duración...!

Intenta resolverlo estimado visitante, es un excelente ejercicio que verdaderamente prueba tus habilidades y destrezas matemáticas.

EXITO!!!

Ejercicio número 15 (pag 41)

Sea n∈ N, n ≥2; y las sucesiones definidas como:

n

Un = ∑ 1/k!
k=0

n
Vn = ∑1/k!+1/n!
k=0

a)Mostrar que las sucesiones (Un) y (Vn) ∀ n ≥2 son dos sucesiones de números racionales

b)Mostrar que (Un) y (Vn) son adyacentes

c)Con un razonamiento por el absurdo, demostrar que su límite común es un número irracional

d)Calcular los 10 primeros términos de ambas sucesiones y verificar que ( U10) es un valor aproximado del número ℮ a 3 x (10)^-8 aproximadamente.

RESUMEN V EDICION DEL CARNAVAL DE MATEMATICAS

Amigos mios me complace en presentar todos los trabajos, articulos, biografias, y demás exposiciones en esta fructifera V edición del carnaval de matemáticas.
He intentado recoger cada una de las exposiciones y hacer el resumen mas completo y sencillo que muestre la escencia de cada trabajo, ustedes me diran si he logrado mi objetivo o me ha faltado algo.

Yo espero haber sido lo suficientemente cuidadoso en recoger debidamente cada entrada, pero si por alguna razon existe uno o más articulos que no he tomado en cuenta les ruego porfavor notificarme para corregir el problema lo mas pronto posible.

Los he clasificado como mejor crei conveniente para facilitar su busqueda y lectura.

Y bueno, sin mas introducción, éstos son los articulos que han participado en esta 5ta edición del carnaval de matemáticas:

1.- SECCION RETOS:

MATEMATICAS DE LA AMISTAD
Tito Eliatron Dixit esta vez nos trae una célebre frase del célebre Sir Francis Bacon, realmente para debatir y pensar en esta curiosa relación aritmética

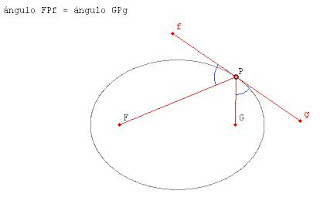
UN SANGAKU “LIGHT”Nuestro amigo E. Gracian desde el blog Sangakoo en una nueva aportación a esta 5ta edición del carnaval de matemáticas nos han propuesto otro interesante problema, esta vez uno de los mas famosos Sangaku´s.



SIMETRIA AXIAL
Manoli en su blog VIAJE A ITACA CON MANOLI nos propone un interesante reto en cuanto a definiciones semánticas versus definiciones técnicas de lo que es SIMETRIA AXIAL para un grupo de estudiantes de escuela tradicional.


MENTALISMO MATEMATICO
Nuestro amigo Rafalillo en su blog EL MUNDO DE RAFALILLO nos trae un interesante juego que sirve para adivinar números para jugar con los panas (amigos) usando “secretamente” ecuaciones de primer grado.


LOS PROBLEMAS DE HILBERT
Nuestro amigo E. Gracian en el Blog Sangakoo expone de manera magistral los 23 grandes problemas de matematicas que fueron planteados por Hilbert el 8 de agosto de 1900 en Paris con motivo del 2do congreso internacional de matemáticas

CALCULO MENTAL DE FORMA INTERACTIVA
Joaquin García en su blog i-matematicas.com nos expone un excelente material pedagógico para potenciar nuestra velocidad en el calculo mental haciendo hincapié en matemáticas interactivas y juegos de razonamiento y velocidad mental

CUADRICULAS MANUALES Y DIGITALES.
Una vez más Javier Omar nos expone interesantes métodos para operar números naturales; inluye un video demostrativo y algunas ingeniosas técnicas.

REGULARIDADES CON PALILLOS DE DIENTES:
Nuestro amigo Joaquin Garcia una vez mas desde su pagina i-matematicas.com nos muestra que los palillos de dientes sirven y de muy buena forma para reconocer regularidades numéricas


DEMOSTRACION DE 1 = 0 Y SIMILARES
Carlos Angosto en su zurditorium nos trae esta vez interesantes demostraciones que muestran que 1 = 0 que 4 = 5 que 1 < 0 … mas demostraciones aquí:

UN PROBLEMA DE INVERSIONES:
El blog de sangakoo nos ha propuesto un interesante reto y ya que estamos en esta 5ta edición del carnaval de matematicas… ¿Quién será el primero en resolverlo? Yo de mi parte aun estoy pensando

2.- SECCION CURIOSIDADES Y DATOS INTERESANTES

¿ERES UN POLIGONAL?
Nuestra amigo Antonio Roldan Martinez en su blog Numeros y Hojas de Cálculo, nos participa su entrada ERES UN POLIGONAL que representa la formula mediante la cual se pueden visualizar algunas propiedades interesantes de los números naturales


EL MUNDO EN CIFRAS
Juan Luis Roldan Calzado en su blog EL ESPEJO LUDICO nos trae algunas cifras super interesantes acerca del comportamiento actual de nuestra sociedad a escala mundial

LA DRA HUESITOS EXPLICANDO MATES
Jesus Soto en su blog LA AVENTURA DE LAS MATEMATICAS nos explica de una manera muy original por medio de la Dra Huesitos, parte de un guion relacionado con ecuaciones de la popular seria BONES, esto de verdad esta interesante

DESAFIANDO A UN GENIO
Evaristo Rodriguez en su blog apuntes matemáticos esta vez nos trae un interesante articulo acerca de cómo el intelecto del matemático indu SRINIVASA RAMANUJAN pudo resolver en treinta segundos un sistema de ecuaciones para muy interesante

MUSICA Y MATEMATICAS
E. Gracian desde el blog de Sangakoo ha participado con esta excelente nota acerca de música y matemáticas, realmente interesante


EL PROBLEMA DE WARING
Miguel Angel Morales Medina en su blog GAUSSIANOS explica este interesante problema planteado por Waring que dice que todo entero positivo puede expresarse como suma de a lo sumo n potencias K-ésimas positivas, siendo n dependiente de K


LA ECUACION DE 2DO GRADO
Carlos Hernandez en su ZURDITORIUM nos explica detalladamente sobre como se llega construir la formula de la ecuación de segundo grado usando el método de completar cuadrados


ESCENAS COMICAS DE MATEMATICAS
Nuestro amigo Trebede en su blog SENTADO EN LA TREBEDE nos demuestra que las matemáticas han sido parte de grandes episodios cineastas y estos excelentes videos que lo prueban se exhiben AQUI


PAPIROS MATEMATICOS
Y nuevamente E. Gracian desde Sangakoo nos ofrece un aporte muy interesante a esta 5ta edición del carnaval de matematicas, esta vez con un estudio sobre los conocimientos matemáticos en Egipto y algunos problemas de la época


MATEMATICAS EN LA BANDERA DE LOS EEUU
Justin Quayle en su blog Justin Quayle nos acerca a un problema bastante curioso ¿Qué pasaría si Pto Rico pasara a formar parte integral de EEUU? Tendrían un pequeño problema con las estrellas de su bandera, incluye un programa en el que se puede ver la distribución de las estrellas en la abndera de acuerdo al número de estados


GEOMETRIA ALGEBRAICA PARA ENCONTRAR EL EQUILIBRIO
Cesar en su blog Experientia docet ha escrito un muy interesante articulo acerca de cómo las matemáticas (en este caso, sistemas de ecuaciones diferenciales de primer orden) son de gran ayuda en reacciones químicas


¿PORQUE NO HAY PREMIOS NOBEL DE MATEMATICAS?
Un excelente articulo de nuestro amigo Cendrero, en su blog "elbustodepalas" su primera aportación a este carnaval de matematicas consiste en resolver el misterio ¿Por qué no otorgan premios Nobel a los matemáticos mas destacados? Descubre el misterio AQUI:

RELOJES PARA MATEMATICOS
Javier Omar nos trae un nuevo aporte a este carnaval, esta vez nos propone un reloj totalmente original… exclusivamente para matematicos


FRONTERAS
Juan Pablo en su blog demairena aprovechando la ocación del mundial nos presenta un interesante análisis acerca de las fronteras geográficas y sus interesantes relaciones matemáticas


BERNAR VENET: ARTE Y MATEMATICAS
Tito Eliatron Dixit en su blog eliatron nos presenta ahora interesantes relaciones entre una exposición artística del frances Bernar Venet (en su exposición La paradoja de la coherencia) y sus toques matemáticos invisibles al común de la gente pero muy interesantes para un matemático entrenado

SIMETRIAS
Una ves mas nuestro amigo E. Gracian del blog sangakoo nos traen un fascinante articulo acerca de simetrias y la perfección que estas representan pero la perfección absoluta sólo puede darse en el reino de las ideas y las abstracciones, un reino en el que las Matemáticas ejercen la soberanía absoluta.


MATEMATICAS, ROCK PROGRESIVO Y FIBONACCI
Nuestro amigo Luis Miguel Iglesias nos trae un interesante articulo que el mismo ha analizado acerca del grupo TOOL mas específicamente el disco Lateralus ¿Cómo esta relacionada la serie de fibonacci en un grupo de rock? Descúbrelo aquí


3.- SECCION BIOGRAFIAS Y MAS ARTICULOS INTERESANTES
HISTORIA MATEMATICA
Javier Omar en su blog COVACHA MATEMATICA nos trae un interesante articulo sobre como dinamizar la enseñanza de la matemática a nivel secundario


MATEMATICOS DE CASTILLA LA MANCHA, SIXTO RIOS
Nuestro amigo Juanmtg nos trae una biografia muy interesante y digna de ser leida por todos acerca del matemático español Sixto Rios, publicado directamente en la pagina del carnaval de matematicas


APORTES DEL MATEMATICO JOHN TUKEY CON MOTIVO DE SU CUMPLEAÑOS
Antonio Gallego en su blog Wank Link Sniper nos aporta sorprendentes detalles acerca de este matemático, químico, estadístico, y pionero informático americano


UN POEMA DE JORGE LUIS BORGES: SOBRE LOS SUEÑOS, EL TIEMPO, LA MUSICA, LAS PALABRAS, LOS NUMEROS
Vaya interesante y muy curioso post, nuestro amigo Pachi Tapiz en su blog Buscando un nombre nos expone un curioso poema del gran Jorge Luis Borges (uno de mis autores favoritos) en los que combina con armonía poetica y presicion matemática algunos términos numéricos


LA MUERTE DEL JOVEN MATEMATICO EVARISTE GALOIS… A SUS 20 AÑOS
Dani, nuestro amigo nos publica en su blog “ese punto azul palido” nos trae una completa biografia del joven matemático Evariste Galois que murió a sus 20 años en un duelo a muerte con un partidario de su misma ideología


CUANDO LAS MATEMATICAS Y LA LITERATURA SE ENCUENTRAN
En su segundo aporte a este carnaval de matematicas, Cendrero en su blog “el busto de palas” nos trae una conjunción entre la matemática y la literatura en forma de versos y poemas


HOOKE & NEWTON
Nuestro amigo Jesus Soto desde su pagina nos cuenta los sucesos que derivaron en la famosa frase “SI HE VISTO MAS ALLA HA SIDO PORQUE ME HALLABA SENTADO EN HOMBROS DE GIGANTES”
Una particular historia de egos y sus originales formas de interpretar una misma cosa contada en dos partes
PARTE 1
PARTE 2


ARQUIMIDES
Una vez mas nuestro amigo E. Gracian del blog de sangakoo nos honran con su aporte esta vez acerca de la biografía y algunos datos interesantes de uno de los padres de la ciencia moderna Arquimides de Siracusa


BIOGRAFIA DEL MATEMATICO ESPAÑOL SIXTO RIOS
Nuestro amigo Juan Martinez nos trae en esta ocación la interesante biografia del matemático Sixto Rios García también conocido como el padre de la estadística española


Tengo resgitradas un total de 36 artiulos en total, existe uno que es la biografia del matemático español Sixto Rios que está registrado en la pagina del carnaval y en un blog, no pude determinar si el autor es diferente, pero con todo he considerado ambas publicaciones.

Me resta agradecer a todos y cada uno de ustedes amigos que han participado en esta V EDICION DEL CARNAVAL DE MATEMATICAS si tienen algun comentario o pregunta acerca de mi trabajo porfavor, estoy abierto a receptar cualquier duda.

Por motivos de tiempo no he podido agradecer a cada uno de ustedes personalmente por sus valiososo aportes, estoy a dos semanas de entrar a examenes finales en la universidad y estoy un poco ajustado de tiempo.

Byron David agradece su participación, nos veremos en la VI EDICION DEL CARNAVAL DE MATEMATICAS

Fue un placer acoger esta V Edición en mi sencillo blog de ciencia, el mundo de Barcedavid

saludos cordiales

BIENVENIDOS A LA V EDICION DEL CARNAVAL DE MATEMATICAS

Estimados visitantes.

Me complace informarles que seré el anfitrión de la 5ta edicion del carnaval de matemáticas, el mismo que tendrá lugar del 14 al 20 de junio proximos.

La forma de participar es muy sencilla, solo debes redactar cualquier artículo que tenga relación con el uso de matemáticas en tu blog, luego deberas notificarme tu entrada dejandome un comentario en este tema para que yo pueda recoger tu aporte, hacer un resumen y adjuntar un link al mismo para que todos puedan leerlo.

El dia 21 de junio realizaré un resumen detallado en la web del carnaval con todos los aportes y sus respectivos links, si no tienes blog dejame un comentario o escribeme un comentario en mi caja de sugerencias para ver como te podemos ayudar.

Todas las preguntas y sugerencias son bienvenidas, dejame un comentario y me pondre en contacto.

Para comodidad de todos los internautas y visitantes de este blog, he colocado un link que te permite compartir en tu espacio favorito cualquiera de mis publicaciones, lo encontrarás al final de cada tema con el titulo "share" y asi puedes compartir estos interesantes temas con quienes desees.

Saludos cordiales

B. David

V EDICION DEL CARNAVAL DE MATEMÁTICAS

La 5ta edición del carnaval de matemáticas esta muy cerca y se estan ultimando los detalles para hacer que esta excelente iniciativa crezca cada vez más entre la comunidad de habla hispana y entre millones de usuarios.

La idea de este proyecto es mostrarle a la gente que las matemáticas en realidad son un mundo maravilloso que a veces se ve opacado por la poca paciencia y dedicación con que nuestros primeros maestros nos enseñaron el mundo de la matemática y la mayoria de nosotros (me incluyo) vimos esta ciencia como algo muy complicado, dificil de entender y mas aún de aplicar en la vida real, afortunadamente la realidad es muy distinta y gracias a la iniciativa del CARNAVAL DE MATEMÁTICAS más gente encuentra muy interesante y curioso cuando se ven las relaciones entre las ciencias exactas y las cosas aparentemente mas triviales de nuestro mundo.

Durante la semana del 14 al 20 de junio se publicarán en los blogs que deseen participar de esta edición; entradas acerca de temas relacionados con matemáticas, y en este blog (que hará de anfitrión de la V edicion del carnaval de matemáticas) se publicará un resumen de todas las entradas y los links a las mismas para que todos los usuarios las puedan leer.

El dia lunes 21 de junio personalmente publicaré en la pagina del CARNAVAL DE MATEMÁTICAS un resumen detallado de todas las entradas participantes en la semana antes mencionada asi como también los links a las mismas.

Saludos cordiales amigos y desde ya les agradezco a todos por anticipado.

B. David

P.D.

Si deseas participar en esta edición porfavor dejame un comentario en este tema o bien dejame un mensaje en la barra de mensajes y nos pondremos en contacto para que puedas participar, se valen todo tipo de publicaciones que tengan relación con MATEMATICAS.

Son muy bienvenidas todas las dudas o sugerencias.

YASUNI - ITT La gran propuesta de un pais pequeño

(para mas informacion visita: http://www.yasuni-itt.gov.ec)

Esta es una propuesta ambiental novedosa y única en el mundo que Ecuador está impulsando desde hace varios años para frenar las emisiones de carbono al aire (CO2) a escala mundial y a su vez transformar su economía de país dependiste en su mayor porcentaje de la extracción y venta de combustibles fósiles a convertirse gradualmente en país con formas económicas mucho mas ecológicas y sustentables.

El yasuní es un parque de biodiversidad natural único en su especie a nivel mundial que tiene una extensión de 982000Ha, según estudios realizados en esta zona una hectárea de este parque contiene más especies de árboles y arbustos que toda américa del norte pero lo más importante es que esta zona es de importancia mundial para la conservación de la biosfera y el equilibrio ambiental del planeta

La propuesta consiste en lo siguiente:

“Debido a que en el campo ITT que se halla en el centro de una zona privilegiada en donde los anfibios, pájaros, mamíferos y plantas vasculares alcanzan su nivel de diversidad máximo en Sudamérica, bajo su tierra existe una reserva de 846 millones de barriles de petróleo por explotar; el estado ecuatoriano se compromete a mantener indefinidamente sin explotar esta importante fuente de combustible mediante certificados de garantía internacional CGY documento financiero perpetuo emitido por el estado ecuatoriano para los contribuyentes y donantes de la iniciativa. Para compensar la falta de ese importante ingreso económico se pide a la comunidad internacional (países desarrollados, corporaciones, filántropos y donantes voluntarios) una compensación monetaria de almenos el 50% de las utilidades (UDS 3500 millones) que significaría el explotar esta zona”

El producto de la venta de estos CGY irá a un fideicomiso internacional el cual se usara para la conservación de más de 40 aéreas protegidas en el Ecuador así como también para la forestación, reforestación y protección de más de 1 millón de bosques en todo el país
De esta forma el planeta se vería libre de almenos 407 millones de toneladas métricas de CO2 lo cual es evidentemente un avance muy significativo en nuestra lucha contra el calentamiento global.

El proyecto es posible y sostenible económica y financieramente, lo cual se manifiesta en varios elementos alternativos y adicionales: canje de deuda, conformación del fondo Yasuní – ITT, construcción del bono Y-ITT y valoración financiera y económica de los beneficios por mantener bajo tierra las reservas extraíbles de crudo del campo ITT.
Dentro de este parque existen dos comunidades en aislamiento voluntario los Tagaeri y los taromenani

Ideas similares son cada vez más popular en toda América del Sur. Brasil ha creado un Amazon Fund, que busca atraer el dinero para conservar la selva tropical - hasta la fecha, Noruega se ha comprometido a aportar hasta $100 millones de dólares durante los próximos años. El gobierno japonés recientemente ha acordado prestar a Perú US $120 millones de dólares para la protección de 212.000 millas cuadradas de selva amazónica en la próxima década. Y Colombia es buscando fondos de Noruega para combatir el cambio climático mediante la protección de sus bosques.

Los países de Europa podrían aceptar los Certificados de Yasuní como equivalentes a los subsidios de carbono negociados en el Intercambio Europeo de la Energía en Leipzig, Alemania. Este es un Mercado para los productos energéticos como la electricidad y el gas natural, así como los derechos para emisión de dióxido de carbono. Pero ese tipo de negociación no está permitida según las reglas del Protocolo de Kioto de 1997, destinado a disminuir las emisiones de gases de efecto invernadero - un tratado que los Estados Unidos rechazó-. Los ecuatorianos esperan que este tipo de proyecto piloto como la Iniciativa Yasuní ITT que propone vender Certificados a cambio de NO emitir carbono a la atmósfera, podría ser aceptado por los países signatarios del protocolo de Kioto

El beneficio para el planeta no es que deje el petróleo bajo la tierra. El beneficio es que se evita emitir CO2, este queda bajo tierra”, agregó. "Así que la idea es: tratar de obtener indemnización, no por el petróleo sino por el carbono evitado
Alemania ha expresado su apoyo a la Iniciativa Yasuní. El Parlamento Alemán aprobó una resolución en junio en favor del proyecto. Ute Koczy, una legisladora del Partido Verde, quien viajó al Ecuador como parte de una delegación para estudiar la cuestión, dijo que otros países, en particular los Estados Unidos, deberían ayudar a encontrar formas de apoyar esta propuesta
El beneficio para el planeta no es que deje el petróleo bajo la tierra. El beneficio es que se evita emitir CO2, este queda bajo tierra”, agregó. "Así que la idea es: tratar de obtener indemnización, no por el petróleo sino por el carbono evitado

¿QUE ES EL YASUNI?

El Parque Nacional Yasuní es uno de los Refugios de Vida del Pleistoceno. Los Refugios del Pleistoceno se formaron durante los cambios climáticos drásticos que tuvieron lugar en el período cuaternario. En este período hubo una alteración entre climas secos y húmedos, en los que las selvas amazónicas crecían o se encogían. En los períodos secos, se formaron islas de vegetación que sirvieron de refugio de especies de flora y fauna, y que constituyeron centros de formación de nuevas especies. Una de estas islas estuvo ubicada en la Amazonía Ecuatoriana, en lo que ha sido declarado Parque Nacional Yasuní.

El Yasuní protege un amplio rango de la comunidad de vegetales arbóreas, considerada como la más diversa del mundo, la cual se extiende desde el occidente del Ecuador y el noreste de Perú hasta el Brasil. 1762 especies de árboles y arbustos han sido descritas en el Yasuní, más de 366 de ellas no han sido clasificadas aún por la ciencia occidental (debido a cambios taxonómicos, nuevos registros para el Ecuador y nuevas especies para la ciencia). La "Zona Intangible" no ha sido bien estudiada, pero otras 116 especies de árboles han sido recolectadas en zonas aledañas. Por lo que se estima que en el Yasuní podrían haber unas 2.244 especies de árboles y arbustos.
Sólo dentro de una hectárea del Yasuní se han encontrado 644 especies de árboles. Para poner este número en perspectiva, hay tantas especies de árboles y arbustos en una hectárea del Yasuní como existen árboles nativos para toda América del Norte, estimado en 680 especies. Se han registrado además, más de 450 especies de lianas y 313 especies de plantas vasculares epífitas.

El Yasuní posee el récord mundial para tierras bajas en el número de epífitas por parcela estudiada. La densidad y abundancia de epífitas en el Yasuní supera los datos registrados en los bosques andinos, en los que se pensaba había la mayor abundancia de plantas epífitas. Por lo menos, el 10% de las especies de epífitas del Yasuní son endémicas a la región del Alto Napo - una pequeña porción del oeste amazónico.

El Yasuní es uno de los lugares más diversos de aves en el mundo, donde se han registrado 567 especies. Protege cerca del 40% de todas las especies de mamíferos de la cuenca amazónica. Este alto porcentaje es notable considerando que los 9.820 kilómetros cuadrados del parque son una miniatura frente a los 6'683.926 kilómetros cuadrados que tiene la cuenca amazónica.

A esto debe sumarse que es el área con el número más alto registrado de herpetofauna en toda Sudamérica, con 105 especies de anfibios y 83 especies de reptiles documentadas. Así como una inmensa diversidad de peces de agua dulce con 382 especies y con más de 100 mil especies de insectos por hectárea.

El 20 de noviembre 1979 se declaró al Yasuní como Parque Nacional. Esta declaración se la hace por existir en su interior una riqueza natural que debe ser preservada.
En 1989 el Parque Nacional Yasuní entra a formar parte de la Reserva Mundial de Biosfera, dentro del programa del Hombre y de la Biosfera de la UNESCO. Como consecuencia de esta declaración el manejo del parque debe estar sujeto a las estrategias de Sevilla, dictadas en la Conferencia de Expertos realizada en España en marzo de 1995. En ellas se determina que en toda reserva de la Biosfera las únicas actividades que se pueden desarrollar, para garantizar el equilibrio y la no contaminación, son: "[...] actividades cooperativas compatibles con prácticas ecológicas racionales, como la educación relativa al medio ambiente, la recreación, el turismo ecológico y la investigación aplicada básica".

En 1999, una parte del Parque fue declarada como "Zona Intangible", el mismo que fue delimitado en el año 2006. Estos son espacios protegidos de excepcional importancia cultural y biológica en los cuales no puede realizarse ningún tipo de actividad extractiva debido a su valor ambiental, no solo para la región, sino para el país y el mundo.
Todas estas categorías de protección fueron otorgadas a este sitio con el objetivo de proteger y preservar innumerables especies animales y vegetales en peligro de extinción, la extensión protegida es de 982.000ha (como ya se indico al inicio de este documento).

El objetivo de crear el parque nacional fue la preservación de especies en peligro de extinción, proteger innumerables especies animales y vegetales, puesto que "cualquier alteración o disminución que sufran los bosques naturales conducen de un modo inevitable a la extinción o menoscabo de la diversidad genética y con ello la degradación de la biodiversidad".

Fuentes:

http://www.eldiario.com.ec/

http://www.amazoniaporlavida.org/

http://www.yasuni-itt.gov.ec/