PARADOJAS MATEMÁTICAS

(ésta entrada participa en la X edición del carnaval de matemáticas cuyo anfitrión para esta edición es Francis (th)E mule Scince's News)

Se llaman PARADOJAS MATEMÁTICAS a ciertos resultados notoriamente falsos que parecen deducirse de demostraciones rigurosas, pero durante las cuales se ha efectuado una operación que no tiene sentido, o un razonamiento erróneo, o una construcción geométrica cuyo trazado no es correcto.

A continuación expondré algunas de ellas:

PARADOJA NUMERO 1:

Sean dos números iguales a y b con "a" elemento de los Naturales y "b" tambien elemento de los Naturales y distintos de cero,  escribiremos:

• a = b

Multipilicando ambos lados de ésta igualdad por el mismo número "a" (lo cuál es absolutamente válido) obtenemos:

• a² = ab

Ahora restamos de ambos lados el mismo número " b² " (lo cuál es absolutamente válido) tenemos:

• a² - b² = ab - b²

Ésta última expresión puede escribirse asi (factorando en ambos lados):

• (a + b)(a - b) = b(a - b)

Dividiendo por (a - b) ya que ambos términos (a y b) son distintos de cero tenemos:

• a + b = b

Pero como al inicio asumimos que a = b entonces podemos escribir:

• b + b = b
• 2b = b

De donde finalmente se obtiene que:

• 2 = 1  ¿?

¿Donde esta el error? El mismo radica en que si asumino al inicio que a y b son elementos del conjunto de los naturales y ambos distintos de cero, ademas que a = b entonces a - b = 0 y la división por cero NO ESTA PERMITIDA de allí que evidentemente 2 no es igual a 1 █

PARADOJA NUMERO 2:

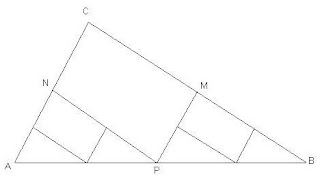
Sea el triángulo ABC y los puntos M, N, P los puntos medios de sus lados.

Tracemos las rectas MP y NP:

Por haberse formado un paralelogramo MPNC resulta:  

AN + NP + PM + MB =AC + CB

Efectuando una construcción análoga para los triángulos ▲ANP y ▲PBM y continuando indefinidamente de este modo, vemos que los segmentos divididos sucesivamente formados tienen siempre su longitud igual a AC + CB.  Como la longitud de los segmentos que forman los segmentos más pequeños disminuye constantemente y sus vértices se aproximan cada vez más a la recta AB decimos entonces que:

En el límite, el perímetro de los segementos divididos llega a confundirse con el segmento AB y por consiguiente:

• AB = AC + CB  ¿?

Esta paradoja se explica por la falsa interpretación del  término <<límite>> cuya definición precisa es:

Se dice que una magnitud variable x tiende hacia un límite determinado A, si los valores sucesivos de x se aproximan al número A de modo que el valor absoluto de la diferencia (x - A) pueda llegar a ser menor que todo número positivo dado, por mas pequeño que éste sea, usando notación matemática se tiene:

Lim (x→a) f(x) = L si para todo ℰ > 0 existe un δ > 0 tal que:

si  0 < │x - a│< ℰ  entonces│f(x) - L│< ℰ

En este ejemplo x y A son respectivamente, el perímetro de los segmentos divididos y la longitud del lado AB. Pero x  es constante y no variable, y la diferencia (x - A) es también constante.

No siendo lícito aplicar la noción de límite a magnitudes que no satisfacen las condiciones de la definición antes descrita; no es de extrañarse pues que en el caso tratado se haya llegado a un resultado por demas ABSURDO! █

PARADOJA NUMERO 3:

Vamos ahora a demostrar con un razonamiento parecido al anterior que una semicircunferencia es igual a su diámetro.

Para esto vamos a trazar dos semicircunferencias que tengan por diámetros los radios OA = OB = R de una semicircunferencia dada. Ésta última Esta última tiene por longitud  πR , y la suma de las otras dos es:

π(1/2 R) + π(1/2 R) = πR  osea igual a la primera.

Continuando con la misma construcción indefinidamente, sse tiene siempre la misma longitud πR para la línea formada por las 4, 8, 16, ... circunferencias, las que por ser cada vez menores, nos inducen a decir que forman una línea que se confunde con el diámetro AB, osea πR = AB █



Saludos cordiales.


Fuentes:
(El hombre que calculaba - Malva Tahan)